Каждый школьник в старших классах сталкивается с таким понятием, как производная. Кажется, что алгебра, которая и так была не самым простым предметом, полностью теряет связь с реальностью. Так как тема традиционно плохо освещена в школьной программе, мы решили написать краткое руководство по производной функции для чайников.
Внимание! Все определения в данной статье являются лишь интерпретацией строгих научных определений и носят ознакомительный характер. Цель данной статьи — дать базовое понимание такого понятия, как производная функция.
Производная и скорость движения точки
Начнем из далека, и это будет очень важно для понимания! Рассмотрим точку, которая движется по известному нам закону. Если скорость движения непостоянная, то координата точки задается некой функцией

К примеру, f(5) - координата в момент времени 5, f(0) - координата в начальный момент времени. Поставим задачу: найти скорость движения в каждый момент времени.
Возьмем, для примера, следующий закон движения:
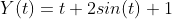
В начальный момент времени наша координата равна

В момент времени 3.14 (число):

Построим график зависимости с помощью Excel:
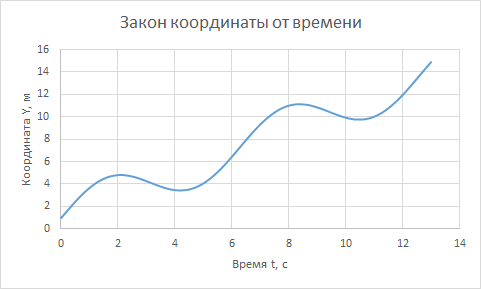
Вернемся к нашей задаче. Из курса физики мы знаем, что скорость на заданном промежутке времени можно посчитать, разделив изменение координаты на длину промежутка времени:

Данная формула определяет среднюю скорость на заданном участке. К примеру, скорость нашего движения за первые 3,14 секунды вычисляется следующим образом:
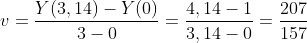
Применим данных подход для нахождения скорости на всем участке движения. Разобьем всё время движения на небольшие промежутки длиной в полсекунды и на каждом из них посчитаем скорость по указанной формуле. Мы получим значения для всех участков. Для наглядности построим график:
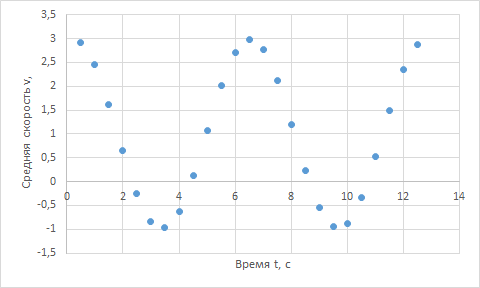
Таким образом мы определили среднюю скорость движения на участках длиной в полсекунды, что практически является решением поставленной задачи. Но что если нам требуется более высокая точность, ведь мы до сих пор ничего не знаем о скорости внутри этих промежутков? Верно: уменьшим длину промежутков: до 0.1 секунды, затем до 0.01 и так далее. Будем уменьшать длину до тех пор, пока длина промежутка не будет бесконечно мала (практически 0) и отрезок можно будет принять за точку. В результате мы получим среднюю скорость на бесконечно маленьком промежутке времени, что по сути является мгновенной скоростью в данный момент времени или просто скоростью в данный момент.
Построим график для полученных значений с помощью Excel:
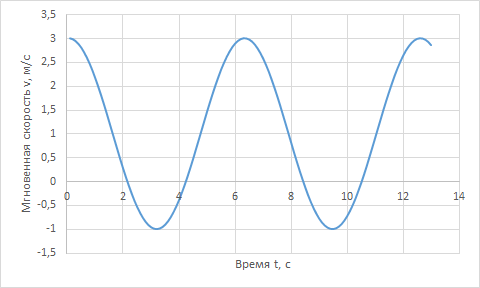
Аналогичным образом считается производная функции, физический смысл которой является мгновенной скоростью изменения функции в данной точке.
Определение производной «на пальцах»
Рассмотрим функцию f [ x [, определенную на отрезке [ a , b ] и произвольные точки Xo и Xo+∆x из интервала [ a , b ].Данный треугольник называется "дельта", он обозначает изменение указанной переменной. Иными словами, вторая точка находится на неком расстоянии ∆x от первой. Длина отрезка [Xo; Xo+∆x] равна ∆x
Вычислим значения функции в указанных точках и найдем разность: f (Xo+∆x) - f(Xo)
Мы получим изменение значения функции на отрезке (Xo; Xo+∆x) (в примере выше это изменение координаты точки за некий промежуток времени). Разделив данную разность на длину промежутка, мы получим среднюю скорость изменения функции на данном отрезке. Теперь устремим длину отрезка к бесконечно маленькому значению, как мы это делали в нашем примере, и получим мгновенную скорость изменения функции.
Данная величина называется производной функции в точке и обозначается f`(Xo)
Иными словами, производная функции в точке — это её мгновенная скорость изменения в данной точке.
Если же существует функция f`(x) , которая в каждой точке [ a , b ] равна производной функции f(x) в данной точке, то говорят, что f`(x) — производная функции f(x)
О том, как данные производные считаются, поговорим в статье «Нахождение производной».
